O que é profundidade de bits no áudio (audio bit depth)?

Atualmente muitos que buscam qualidade no áudio ou músicas de qualidade, não deixam de citar os arquivos "Hi-Res", os FLAC 24 bits e os MQA (master quality audio). Esta é uma tendência cada vez maior nos smartphones topo de linha que tentam oferecer uma qualidade de áudio maior tanto em seu DAC quanto no suporte a codecs de áudio Bluetooth avançados como o LDAC, desenvolvido pela Sony. Além disto, ainda há os serviços de streaming de músicas que prometem uma qualidade de áudio sem perdas como, por exemplo, o Tidal.

A promessa dita pelos fabricantes de equipamentos de áudio, de desenvolvedores de formatos de transmissão de áudio e de streaming de música, é simples: qualidade de áudio superior devido à maior quantidade de dados, também conhecidos como profundidade de bits, ou bit depth em inglês. São 24-bits de 1 e 0 contra os meros 16 bits do CD. Evidentemente estes arquivos de alta resolução custam mais caro devido a sua qualidade, mas quanto mais bits, melhor é o resultado ao ouvir a música, certo?

Bom, a resposta para a pergunta acima é: não necessariamente. O argumento de um valor na profundidade de bits cada vez maior não é baseado em algo científico, mas na distorção do que realmente ocorre e na exploração da ignorância do consumidor sobre a mídia que ele está consumindo. Ou seja, é um fato que as lojas que comercializam faixas em 24 bits lucram muito mais do que entregam uma real melhora na qualidade sonora prometida.

Profundidade de bits (bit depth) e qualidade de som

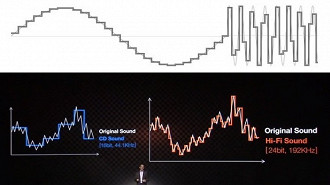
O maior exemplo que as empresas que comercializam áudio em 24bits é a demonstração de uma onda senoidal serrilhada, como se fossem escadas. Ao observarmos um arquivo que está com resolução 16 bits, vemos uma linha irregular, mas quando olhamos para a mesma música em 24 bits, parece uma linha praticamente suave, com uma definição melhor. É uma ilustração visual básica, mas que dependendo do conhecimento sobre o assunto que a pessoa tiver, ela pode ser facilmente enganada.

Os exemplos das linhas em formato de escadas não são de todo ruins, pois mostram com uma certa precisão como o áudio digital se comporta. Entretanto, se for utilizado um gráfico de trama de hastes, será possível ver com mais acurácia visual do que as linhas em formato de escadas utilizada.

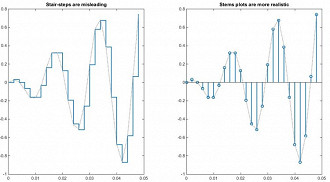
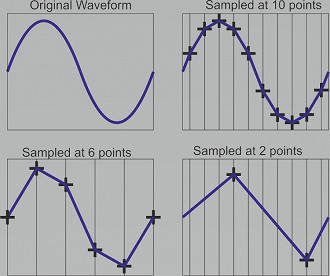
Para ficar mais fácil de entender, pense no conceito de taxa de amostragem (sample rate) e analise a amplitude de uma amostra (sample) em um único ponto da reprodução do arquivo. Quanto menor o espaçamento entre as hastes, maior será o número de registros de samples por segundo, gerando assim um nível de profundidade de bits mais alto.

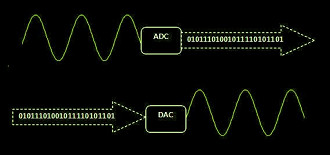
Entretanto, sabe-se que um conversor de sinal analógico para digital (ADC ou analog to digital converter) precisa ajustar o sinal de áudio analógico que é infinito em um número finito (limitado) de bits. Isso ocorre ao gravar um som com o microfone e transformar as ondas sonoras geradas (som analógico) em digital (composto de 0 e 1).

Quando o ADC tenta converter um sinal analógico em digital, pode ocorrer de um bit cair entre dois níveis e ser arredondado para algo que seja mais próximo. Isto é conhecido como erro de quantização (quantization error) ou ruído de quantização (quantization noise).

Porém, ao analisar qualquer saída de áudio de um DAC (digital to analog converter) recente, presente em todos os equipamentos reprodutores de som, você não conseguirá ver escada alguma como foi desenhada nos gráficos acima (mesmo que o sinal emitido seja em 8 bits). Então, de onde tiraram este gráfico em escadas?

Os diagramas em degraus servem para se descrever o zero-order-hold DAC (DAC de ordem zero). Esta tecnologia de DACs é muito simples e barata, onde um sinal sofre alternação entre vários níveis a cada nova amostra para gerar uma saída. Este tipo de chip não é utilizado em produtos de áudio profissional ou descentes para o consumidor. Você pode achá-lo em um microcontrolador por exemplo.

DACs e ADCs utilizados para a reprodução de áudio são na grande maioria das vezes baseados na modulação delta-sigma (∆Σ). Os DACs deste tipo convertem amostras de áudio em um fluxo de 1 bit (modulação de densidade de pulso ou pulse-density modulation) com uma taxa de amostragem muito alta. Ao realizar a filtragem, o conversor produz um sinal suave com o ruído filtrado de frequências audíveis.

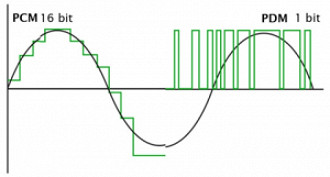
Ou seja, um DAC atual não produz amostras de áudio com irregularidades, por pior que ele seja. Na verdade, eles produzem um fluxo de bits que recebe uma filtragem de ruído para ter uma saída precisa e suave. O gráfico de escadas está errado por conta do "ruído de quantização".

O que é o ruído de quantização (quantization noise)?

Em qualquer sistema finito ocorrerão erros de arredondamento. Pensando nesta linha, é verdade que um DAC ou um ADC de 24 bits terá uma chance de erro de arredondamento menor do que um de 16 bits. Mas o que isso quer dizer na realidade? Ou melhor, o que realmente será percebido por nossos ouvidos? É uma granulação ou distorção? Os detalhes são perdidos?

O que acontece é a ocorrência de ambos, a depender se você está no meio digital ou analógico. De qualquer forma, o conceito para entender melhor isto é entender como funciona o nível de ruído e como ele diminui à medida que a profundidade de bits aumenta (bit depth).

Para entendermos melhor como isto acontece, precisamos observar alguns pontos. O primeiro deles é o da imagem abaixo, onde temos uma onda de entrada (input), analógica, na cor azul, e uma onda quantizada, digital, na cor laranja. Estas duas ondas estão demonstradas em 2, 4 e 8 bits. Para exemplificar melhor, foi adicionado uma pequena quantidade de ruído ao sinal, na tentativa de simular melhor o que realmente acontece.

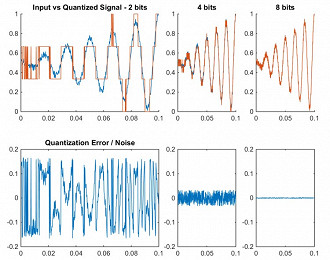
Observe que na parte mais abaixo da imagem, onde há somente a onda azul, está sendo medido o erro de quantização (ou de arredondamento), que é calculado a partir da subtração do sinal quantizado (sinal digital que foi arredondado a partir da onda analógica) do sinal de entrada (onda analógica).

Note que ao aumentar a profundidade do bit, o sinal quantizado (digital) corresponde melhor ao sinal de entrada (analógico). Entretanto, este fato não é importante e sim o fato de que o sinal de erro (ruído) é maior nos bits mais baixos. O que ocorreu não foi a remoção de dados do sinal de entrada e sim a adição de ruído no sinal. A síntese aditiva (Additive Synthesis) nos fala que um sinal pode ser reproduzido pela soma de quaisquer outros sinais, incluindo sinais fora de fase que acabam por subtrair partes do sinal original. É desta forma que ocorre o cancelamento de ruído ativo. Ou seja, os erros de arredondamento adicionam um novo ruído de sinal.

O que foi dito acima sobre ruído, não é apenas teórico, você realmente percebe um nível de ruído cada vez maior quando os arquivos de audio possuem uma profundidade de bits muito baixa. Além disto, não é possível capturar um sinal (sample) menor do que uma etapa de quantização. Pequenas mudanças de sinal precisam passar para um nível de quantização o mais próximo possível e por isso, uma profundidade de bits maiores consegue um melhor desempenho (possui etapas de quantização menores, que é um espaço mais curto entre uma sample e outra).

Outra coisa que se deve levar em consideração, é a amplitude do ruído de quantização, que permanece a mesma, independente da amplitude do sinal de entrada. Isso mostra que o ruído ocorre em qualquer nível de quantização. Ou seja, é certo falar que independente da profundidade de bits, há um certo nível de ruído que é constante. Sendo assim, profundidade de bits maiores produzem menos ruído. Isto nos faz pensar sobre onde está situado o ponto de equilíbrio em que não irá haver um ruído perceptível e não se tem uma profundidade de bits exagerada, pois como você já deve ter visto, arquivos com 24 bits ou 32 bits, são consideravelmente maiores.

A profundidade de bits (bit depth) está diretamente ligada ao ruído

Como já sabemos que o ruído pode interferir em nossos arquivos de música e como ele se comporta de acordo com a profundidade de bits, vamos analisar novamente o gráfico de exemplos de áudio em 2,4 e 8 bits. Note que quando reproduzimos o arquivo de 8 bits, temos uma correspondência quase perfeita com o sinal de entrada (linhas azuis e laranja). Isso ocorre porque a profundidade de 8 bits já é o suficiente para capturar o nível de ruído de fundo. Ou seja, a etapa de quantização (laranja) é menor que a amplitude sinal de entrada (azul) ou a relação sinal-ruído (SNR) é melhor do que o nível de ruído de fundo.

A equação do SNR é a equação 20log (2n), onde n é a profundidade de bits. Um sinal de 8 bits possui um SNR de 48dB, 12 bits já possui 72dB, 16 bits pode gerar 96dB e 24 bits 144dB. Com isto sabemos agora o que é preciso para inserir a faixa dinâmica (dynamic range) entre o ruído de fundo e o sinal mais alto que se pretende capturar (gravar com microfone) para reproduzir da melhor forma possível o som.

O nosso ouvido possui uma sensibilidade que varia entre 0dB (silencio) até aproximadamente 120dB (som extremamente alto, que chega a causar dor). Além disto, a nossa capacidade de perceber mudanças no volume é de 1dB, ou seja, o alcance dinâmico (dynamic range) do ouvido humano é de 20 bits, que equivale a 120dB. Entretanto, é um fato que você não pode ouvir um som nesta altura por muito tempo, pois isso causaria danos irreversíveis como você pode ver abaixo.

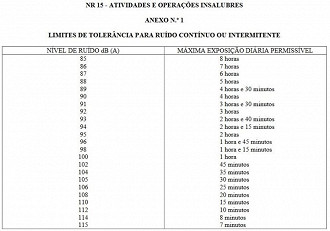
Além do fato de termos de lidar com o nível excessivo de decibels, à medida que se aumenta o volume, ocorre o mascaramento das frequências mais altas (agudos) em nosso ouvido. Isso não acontece quando se ouve em volumes baixos como a 20 ou 40 decibels, com a exceção de sons próximos demais. Mas ao colocarmos em um volume de 80db, há uma perda dos sons abaixo de 40db, assim como se colocarmos a 100dB, há um mascaramento das frequências abaixo de 70dB.

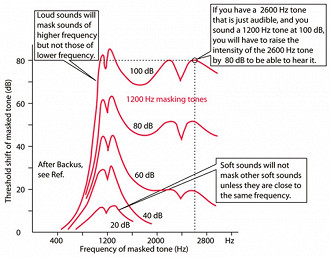
A dinâmica dos nossos ouvidos e os arquivos dos materiais de audição dificultam o fornecimento de um número preciso, mas a faixa dinâmica real aproximada do ouvido humano está na região dos 70dB em um ambiente com ruído médio, e somente 40dB em ambientes com muito ruído. É provável que uma profundidade de apenas 12 bits já fosse o suficiente para a grande maioria das pessoas. Ou seja, um CD de 16 bits já é mais que o suficiente.

Grande maioria dos instrumentos de som e microfones de gravação também geram ruídos (principalmente os amplificadores de guitarras), mesmo em estúdios com salas bem tratadas (com um nível de ruído consideravelmente baixo). Existem estudos sobre a faixa dinâmica dos diferentes gêneros musicais, onde nos mostra que a maioria possui a média de 60dB. Músicas mais "calmas" como coral, opera, piano, possuem faixas dinâmicas (dynamic range) máximas de aproximadamente 70dB, enquanto o rock, o pop e o rap, por exemplo, apresentam um DR de 60dB ou menos.

Apesar do que foi dito acima, a indústria da música na grande maioria das vezes acaba distorcendo a qualidade das músicas, comprimindo muito o áudio (aumentando o ruído e atenuando os picos), na tentativa de aumentar o volume geral das faixas, para causar mais "emoção". Entretanto, isso acaba reduzindo a faixa dinâmica das gravações (dynamic range) e mascarando as frequências, devido ao excesso de trechos com dB alto.

Porque utilizar arquivos de áudio em 24 bits ou superior?

A utilidade da utilização de alto nível profundidade de bits se volta para os estúdios, pois a cada filtro e conversão que se aplica, o ruído de fundo aumenta. Este aumento do ruído ocorre devido a inserção de uma nova onda, como foi explicado acima. Ou seja, ao utilizar um nível de profundidade de bits maior (bit depth) o engenheiro de som evita que o áudio original gere ruído ao manipulá-lo na mixagem e masterização.

Entretanto, lembre-se que isto será mais útil para a produção do áudio e não para o ouvinte, como foi explicado acima.

Conclusão

O que fará a diferença será o equilíbrio entre os sons feito na masterização e não a profundidade de bits em si, já que os 16 bits do CD já são mais que suficientes para os ouvintes da música.

Artigos recomendados:

• Especificações: Diferença entre taxa de amostragem, resposta de frequência e alcance de frequência
• Saiba a diferença entre MP3, FLAC, Opus e AAC
• O que é áudio Hi-Res? Conheça o novo áudio em alta resolução
• Saiba o que influencia na qualidade do arquivo de música

Esse artigo é feito em parceria com o Grupo Fones de Ouvido High-End:

• Página da Fones de Ouvido High-End
• Grupo Fones de Ouvido High-End
• Grupo Fones de Ouvido Low-End
• Grupo Fones de Ouvido High-End Store
• Instagram: @foneshighend